莫里斯遍历

发表于 更新于 分类于 阅读次数： 本文字数： 2.2k 阅读时长 ≈ 2 分钟

本文写于 2020 年 5 月 3 日，2022 年 3 月 20 日重新整理

莫里斯遍历 (Morris Traversal) 是一种时间复杂度为 O(n) ，空间复杂度为 O(1) ，且不改变树的结构的二叉树遍历算法。

莫里斯遍历

通常的二叉树遍历算法使用堆栈或者递归完成，它们的空间复杂度通常是 O(n) 的。
要使用 O(1) 的空间实现遍历，最主要的难点是如何在指针到达叶节点的时候回到父节点，在不能使用堆栈的情况下，莫里斯遍历使用线索二叉树 (Threaded Binary Tree) 的思想，莫里斯方法中不需要额外的空间来保存叶子节点的前驱 (predecessor) 节点和后继 (successor) 节点，只需要利用叶子节点的空闲左右子节点按照一定的顺序指向前驱或后继节点就可以。

首先看莫里斯方法的中序遍历，通过中序遍历可以推出其他顺序的遍历。

首先实现一个 LeetCode 风格的二叉树节点原型：

1
2
3
4
5
6
struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int _val):val(_val),left(NULL),right(NULL){ }
}

中序遍历

算法流程：

  1. 如果当前节点的左子节点为空，则访问当前节点并以当前节点的右子节点作为当前节点（与普通遍历无异）
  2. 如果当前节点的左子节点不为空，则在当前节点的左子树中寻找当前节点在中序遍历下的前驱节点
    1. 如果前驱节点的右子节点为空，则将它的右子节点设置为当前节点（设置线索）。更新当前节点为当前节点的左子节点
    2. 如果前驱节点的右子节点为当前节点，则将其重设为空（断开线索，恢复树的形状）。访问当前节点并更新当前节点为当前节点的右子节点。
  3. 重复以上两点直到当前节点为空。
    线索设置和遍历过程图示:

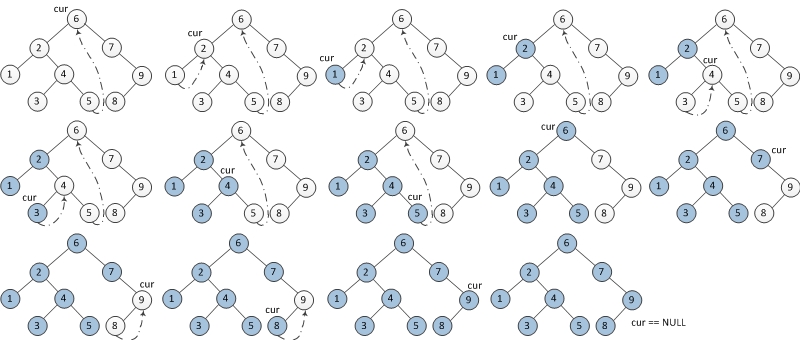
代码过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void visit(TreeNode *root);

void inOrderTraversal(TreeNode *root)
{
    TreeNode *cur = root;
    TreeNode *prev = NULL;
    while (cur != NULL) {
        if (cur->left == NULL) { //最左侧
            visit(cur);
            cur = cur->right;
        }
        else {
            prev = cur->left;
            while (prev->right != NULL && prev->right != cur) //find the predecessor
                prev = prev->right;
            if (prev->right == NULL) {
                prev->right = cur;
                cur = cur->left;
            }
            else if (prev->right == cur) { //recover
                prev->right = NULL;
                visit(cur);
                cur = cur->right;
            }
        }
    }
}

算法的空间复杂度是 O(1) 的，时间复杂度主要体现在寻找前驱节点的操作上：

1
2
while (prev != NULL && prev->right != NULL) //find the predecessor
    prev = prev->right;

这段代码的时间复杂度直观上是 O(log n) 的，但是由于要对每个左子节点非空的节点都要做一次，因此总体上是 O(n) 的。

前序遍历

前序遍历与中序遍历总体上是相同的，只是访问节点的时机略有不同

算法流程：

  1. 如果当前节点的左子节点为空，则访问当前节点并以当前节点的右子节点作为当前节点（与普通遍历无异）
  2. 如果当前节点的左子节点不为空，则在当前节点的左子树中寻找当前节点在中序遍历下的前驱节点
    1. 如果前驱节点的右子节点为空，则将它的右子节点设置为当前节点（设置线索）之后访问当前节点。更新当前节点为当前节点的左子节点
    2. 如果前驱节点的右子节点为当前节点，则将其重设为空（断开线索，恢复树的形状）。更新当前节点为当前节点的右子节点。
  3. 重复以上两点直到当前节点为空。
    代码过程：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void preOrderTraversal(TreeNode *root)
{
    TreeNode *cur = root;
    TreeNode *prev = NULL;
    while (cur != NULL) {
        if (cur != NULL) {
            visit(cur);
            cur = cur->right;
        }
        else {
            prev = cur->left;
            while (prev->right != NULL && prev->right != cur)
                prev = prev->right;
            if (prev->right == NULL) {
                prev->right = cur;
                visit(cur);
                cur = cur->left;
            }
            else {
                prev->right = NULL;
                cur = cur->right;
            }
        }
    }
}

Reference

Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间）