数据结构--二叉树和二叉树的储存结构

本文写于 2020 年 3 月 24 日，2022 年 3 月 6 日重新整理

定义

二叉树是一个有穷的节点集合，这个集合可以为空。若集合不为空，则集合是由根节点 root 和被称为左子树和右子树的两颗不相交的二叉树组成。

特殊二叉树

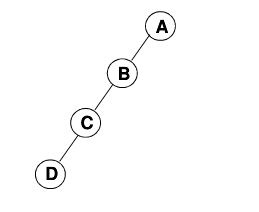
• 斜二叉树 (Skewed Binary Tree)
  如图：

• 完美二叉树 (Perfect Binary Tree) 或满二叉树 (Full Binary Tree)

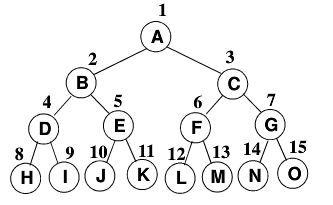
• 完全二叉树 (Complete Binary Tree)

  有 n 个节点的二叉树，对树中节点按从上到下，从左到右的顺序进行编号。与满二叉树相比，相同位置处的节点编号相同。

  即：完全二叉树相当于满二叉树少了最下层叶子节点的右侧若干节点。

性质

• 二叉树的第 i 层最大节点个数为 $2^{i - 1}$
• 深度为 k 的二叉树最大节点总数为 $2^k - 1$
• 对于任何非空二叉树 T ，若 $n_0$ 表示叶节点的个数， $n_2$ 是度为2的非叶节点的个数，那么两者满足关系 $n_0 = n_2 + 1$

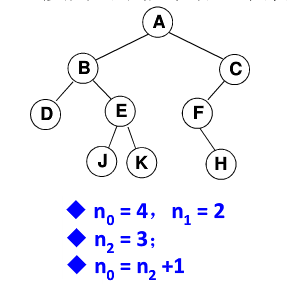
证明：对于总结点数为 n 的二叉树，其边总数为 n-1 。总的节点数 n 由度为 0,1,2 的节点组成，即 $n - 1 = n_0 + n_1 + n_2 - 1$ 。

同时，对于二叉树的节点，其度数即为其对总边数的贡献值，即：度为 i 的节点将贡献 i 条边。所以边数 n-1 满足 $n - 1 = 0\times n_0 + 1\times n_1 + 2\times n_2$ 。

所以 $n-1 = n_0+n_1+n_2 - 1=0\times n_0+1\times n_1 + 2\times n_2$ ，即： $n_0 = n_2 + 1$ 。

ADT描述

操作集

bool isEmpty(BinaryTree* tree);     //判断二叉树是否为空
BinaryTree* createBinaryTree();     //创建一个二叉树
void traversal(BinaryTree* tree);   //遍历二叉树

对于二叉树而言，遍历是其最重要的操作。常见的遍历方法有：

void preOrderTraversal(BinaryTree* tree);   //先序遍历，根--左子树--右子树
void inOrderTraversal(BinaryTree* tree);    //中序遍历，左子树--根--右子树
void postOrderTraversal(BinaryTree* tree);  //后序遍历，左子树--右子树--根
void levelOrderTraversal(BinaryTree* tree); //层次遍历，从上到下，从左到右

储存结构

顺序结构

• 对于完全二叉树，对其按从上到下，从左到右的顺序进行编号：

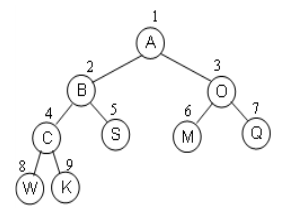
如图不难看出，父节点的编号为 i 时，其左子节点的编号为 2i ，其右子节点的编号为 2i+1 ，父节点的编号是子节点编号除以 2 的向下取整。

对于这样的二叉树，我们可以定义一个长度合适的数组来储存数的数据，由于其节点编号的规律性，树的遍历等操作不会困难。

节点	A	B	O	C	S	M	Q	W	K
编号	1	2	3	4	5	6	7	8	9

• 对于一般二叉树，也可以用这样的方式储存。不过首先需要把非完全二叉树用空节点变为完全二叉树：

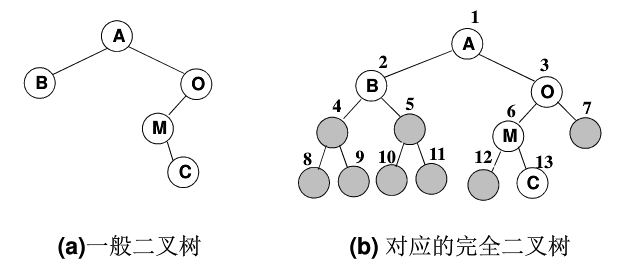
用数组储存为：

节点	A	B	O	null	null	M	null	null	null	null	null	null	C
编号	1	2	3	4	5	6	7	8	9	10	11	12	13

可见，数组结构的二叉树会造成一定的空间浪费。

链式结构

将节点设计成如图样式，内部储存节点数据和指向左右子节点的指针。

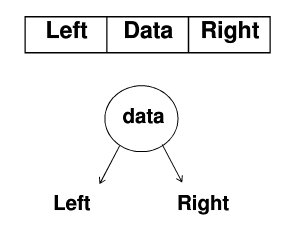
typedef struct binaryTree{
    ElementType data;
    BinaryTree* left;
    BinaryTree* right;
}BinaryTree;